多维尺度MDS案例

• 1、背景

  当前有中国有8大核心城市的距离数据，希望使用多维尺度法直观展示该8大城市的距离情况，数据如下图所示：

  

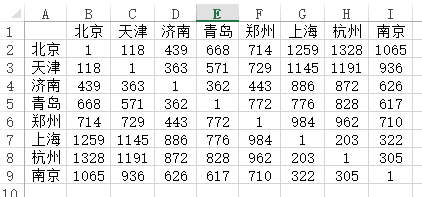
  图中右下角数据为1，其代表自己，以及数据呈现出完全对称关系。上述数据中数字代表实际距离，因而应该使用‘度量MDS法’，并且数据格式为n*n格式。可选择‘计算欧氏距离’。

• 2、理论

  多维尺度MDS涉及2种类型，分别是度量MDS和非度量MDS，以及SPSSAU支持两种数据格式。具体如下事例说明：

  如果研究的是‘饮料口味相似度’，类似下图这样的n*n结构数据，数字代表的距离只是一种‘次序’非实际距离（比如coffee和milk之间的数字为6代表距离较远，但beer和wine之间的数字为1代表距离非常近），此类数据一般使用‘非度量MDS’法，数据格式为n*n结构数据；

  

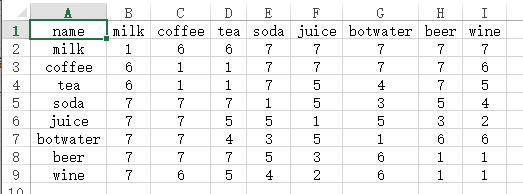
  除此之外，还有一种数据为‘原始数据’格式，比如研究中国31省市在8个维度的消费情况，以便可视化呈现各省市居民的相似情况，如下图所示：

  

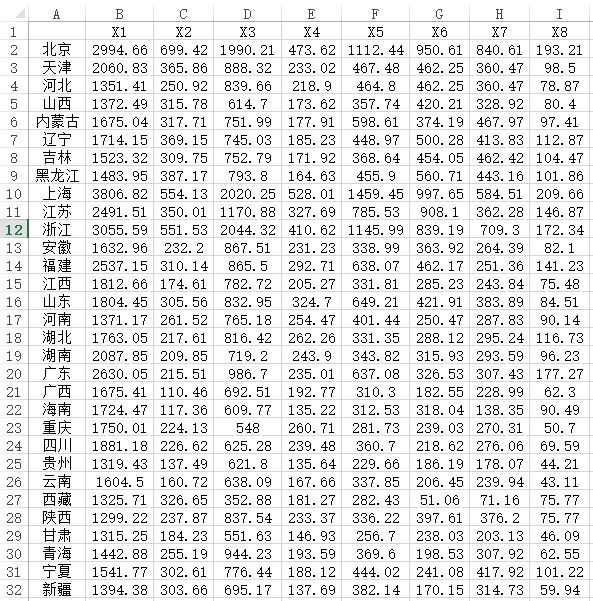
  上图展示中国31省市在8个维度上的消费数据，数字代表实际消费情况，因此此类数据应该使用‘度量MDS’，而且选中‘计算欧氏距离’，而且上述图中数据格式为‘原始数据’格式，其并非n*n格式数据。

• 3、操作

  本例子操作如下：

  

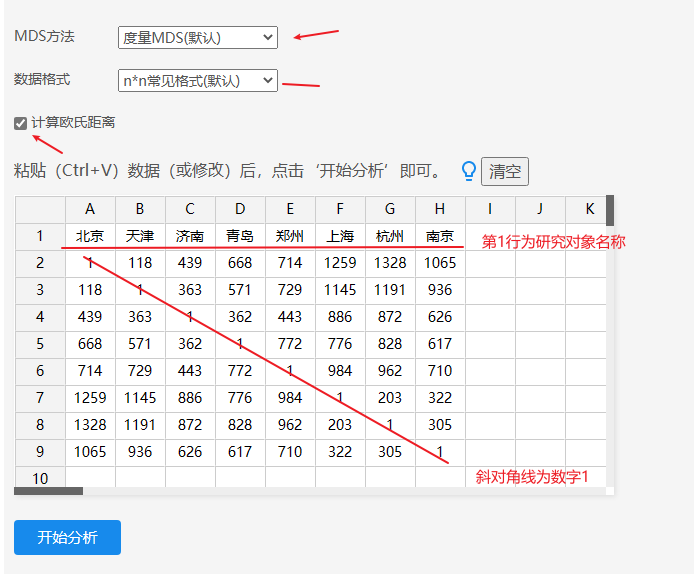
  由于数字为实际距离值，因而使用‘度量MDS’法，并且选中‘计算欧式距离’，以及当前数据格式为n*n格式。

• 4、SPSSAU输出结果

  SPSSAU共输出2个表格和1个图。分别如下说明：

  表格或图	说明
  基本参数设置	即模型的基本设置参数情况
  模型维度数据结果	可视化图维度的坐标数据
  MDS距离模型	MDS距离模型可视化图

• 5、文字分析

  基本参数设置
  MDS方法类型	数据格式	是否计算欧式距离	维度数量
  度量MDS	n*n格式	是	2

  上表格展示MDS模型的基本设置，本次案例使用度量MDS法进行研究，输入数据为n*n格式，并且要求先计算欧式距离后再进入模型分析。

  

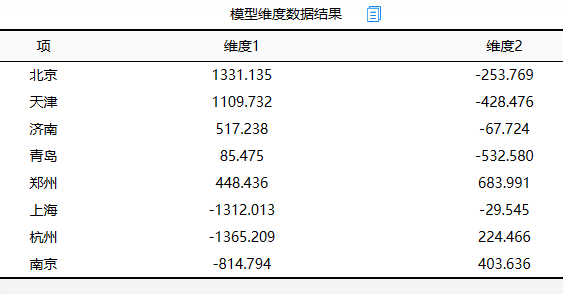
  上表格MDS距离模型的具体坐标数据，下图为MDS距离模型，图示可以看见北京和天津的距离非常近，而且上海和杭州的距离很近。但郑州离其余七个城市均有很远的距离，这与事实情况完全吻合。足以证明MDS模型可以很好的可视化展示距离数据。

  

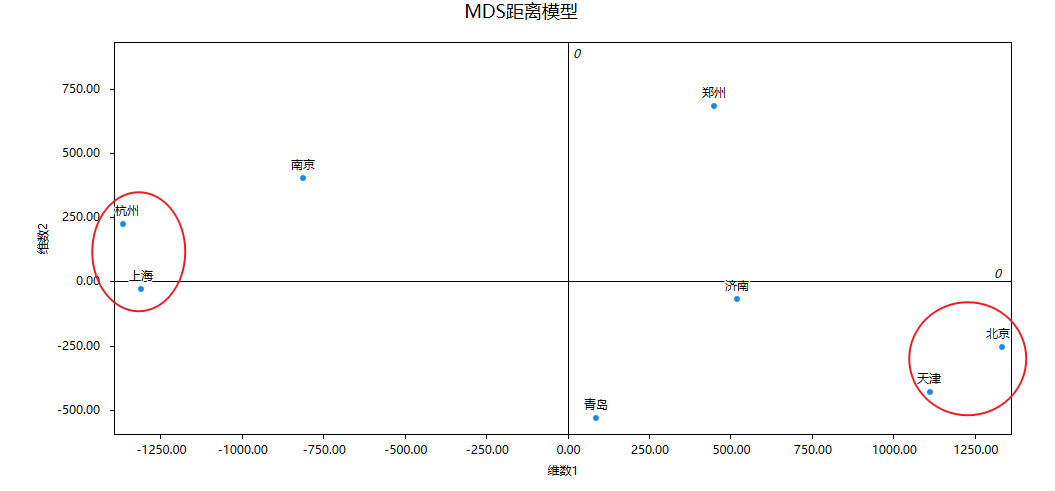
• 6、剖析

  涉及以下几个关键点，分别如下：

  • 关于SPSSAU中‘计算欧式距离’参数？

  • 如果是度量MDS数据，可选中‘计算欧式距离’，即让系统先计算出各研究对象之间的欧式距离后然后进入模型进行分析，当然这由研究者自身决定，通常需要选中计算。

  • 如果提供的是‘原始数据格式’（非n*n格式时），此时系统自动会计算出各研究对象之间的欧式距离，然后构建出数据后进行MDS距离模型计算，此时不论是否选中‘欧式距离’，系统会会先进行研究对象欧式距离计算后再进入MDS模型。