空间计量研究中，空间杜宾误差模型，其考虑两项，分别是自变量X的空间滞后作用，以及误差扰动项的空间滞后作用，其数学模型公式如下：

y = β_k * x + θ_k * W_x + u, u = λ * W_u + µ（其中β_k表示X的回归系数，W_x表示自变量X空间滞后变量，θ_k表示W_x的回归系数，W_u表示u的空间滞后变量，λ表示W_u的回归系数，u和µ为扰动误差项）

• 1、背景

  当前有一份空间数据，其为美国哥伦布市49个社区的相关数据，包括犯罪率（crime）、房价（hoval）和家庭收入（income），当前希望研究房价和家庭收入对于犯罪率的影响关系，并且在研究这一影响关系时，考虑空间性，希望使用空间杜宾误差SDEM模型进行分析。部分数据如下图所示：

  

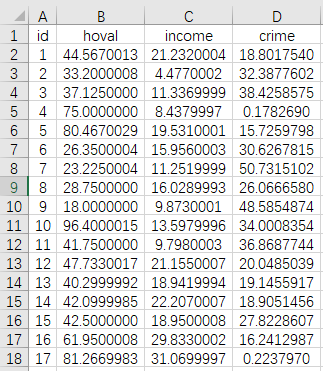
  上面展示的是‘分析数据’，共有49个社区，该49个社区对应的‘空间权重矩阵’如下图所示：

  

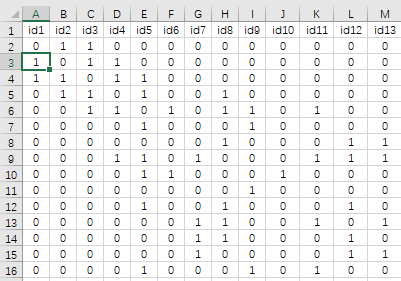
  图中数字1表示两个空间点（社区）之间相邻，数字0表示两个社区不相邻。空间权重矩阵数据可点击此处下载。

• 2、理论

  空间杜宾误差模型SDEM的自变量包括X， W_x即自变量空间滞后变量，其意义为当前Y受到空间相邻地区X的影响作用，以及还有误差项空间滞后项，其意义为Y无法解释部分的空间项。其数学模式公式如下：

  y = β_k * x + θ_k * W_x + u, u = λ * W_u + µ（其中β_k表示X的回归系数，W_x表示自变量X空间滞后变量，θ_k表示W_x的回归系数，W_u表示u的空间滞后变量，λ表示W_u的回归系数，u和µ为扰动误差项）

• 3、操作

  本例子操作如下：

  

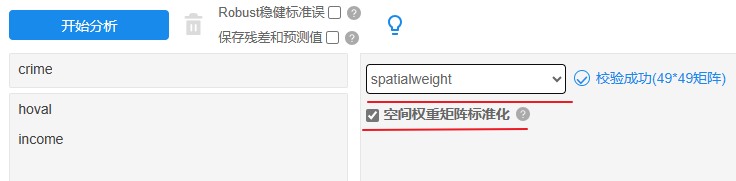
  下拉选择‘空间权重矩阵’文档即spatialweight这份数据，默认对空间权重矩阵行标准化处理，需要注意的是，空间权重矩阵通常需要进行行标准化处理。

  另需要提示的是，在使用空间计量相关的方法时，其均需要‘空间权重矩阵’和‘分析数据’两份数据，并且均需要单独上传到SPSSAU中，并且对‘分析数据’进行分析时，下拉选择对应的‘空间权重矩阵’，操作上分为以下3个步骤。

  • 第1：上传‘空间权重矩阵’文档

    此处需要注意：上传的数据需要为n*n阶格式，而且第1行为空间点的名称（比如31省市的名称）。类似下图格式：

    

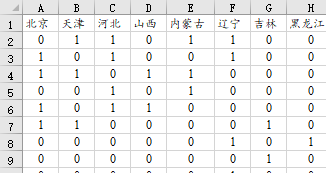
  • 第2：上传‘分析数据’文档

    此处需要注意：比如31省市数据，‘空间权重矩阵’有着该31个空间点的顺序比如北京-》天津-》河北-》山西-》…，那么‘分析数据’的31行数据也需要按此顺序才可以。

  • 第3：针对‘分析数据’进行分析，并且选择‘空间权重矩阵’文档

    此处需要注意：进行某空间研究方法时需要下拉选择‘空间权重矩阵’，选择后，SPSSAU会自动判断其是否为‘空间权重矩阵’格式，包括是否为n*n阶结构，是否具有对称性等。如果不是则会进行信息提示，请勿必注意空间权重矩阵数据格式。

• 4、SPSSAU输出结果

  SPSSAU共输出6个表格，分别是模型基本参数等、空间杜宾误差SDEM模型分析结果、空间杜宾误差SDEM模型相关检验汇总、信息准则指标结果、空间效应分析和空间杜宾误差SDEM模型分析结果-简化格式表格，如下所述。

  表格	说明
  模型基本参数等	输出模型的基础参数值信息等
  空间杜宾误差SDEM模型分析结果	输出模型的分析结果，包括回归系数和显著性检验结果等
  空间杜宾误差SDEM模型相关检验汇总	输出相关的检验比如异方差检验等
  信息准则指标结果	如果是极大似然ML法时则会输出信息准则指标等
  空间效应分析	输出空间效应分析表格
  空间杜宾误差SDEM模型分析结果-简化格式	输出模型结果的简化表格格式

• 5、文字分析

  

  上表格模型的基本参数信息，包括具体的空间计量模型名称，是否使用稳健标准误差，空间权重矩阵名称及是否对其进行标准化处理等，模型估计方法等，表格中仅展示模型的参数信息等无特别分析意义。需要注意的是，当前默认使用ML极大似然法进行估计，但当选中Robust稳健标准误法时，则使用GMM估计，GMM估计法时不会输出llf指标等，即其会影响到后续输出信息准则指标表格。

  

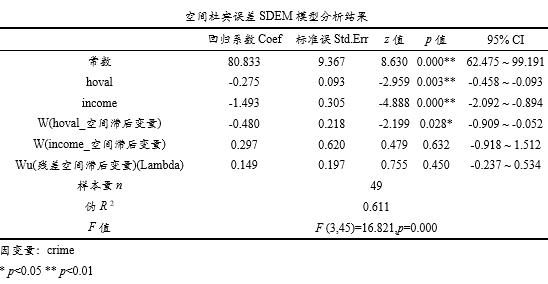
  上表格展示空间杜宾误差SDEM模型回归结果，其数学模型为y = β * x + θ * W_x + u, u = λ * W_u + μ (其中β表示X的回归系数，W_x表示自变量X空间滞后变量，θ表示W_x的回归系数，W_u表示u的空间滞后变量，λ表示W_u的回归系数，u和μ为扰动项)，结合当前数据，其公式为：crime = 80.833-0.275*hoval-1.493*income-0.480*hoval_空间滞后变量+0.297*income_空间滞后变量+0.149*残差空间滞后变量。

  具体针对各项的影响关系来看：hoval的回归系数值为-0.275，并且呈现出0.01水平显著性(p =0.003<0.01)，意味着hoval会对crime产生显著的负向影响关系，即说明房价会负向影响犯罪率，房价越高犯罪率越低。income的回归系数值为-1.493，并且呈现出0.01水平显著性(p =0.000<0.01)，意味着income会对crime产生显著的负向影响关系，家庭收入越高犯罪率越低。

  除此之外，房价的空间滞后变量，其回归系数值为-0.480，其p 值为0.028<0.05，意味着其他地区的房价会影响到当前地区的犯罪率，其他的房价越高，本地区的犯罪率反而会越低。家庭收入空间滞后项没有呈现出显著性，即说明其他地区家庭收入并不会对于本地区的犯罪率产生影响。与此同时，误差项滞后变量并没有呈现出显著性，意味着误差项并没有空间作用机制。

  

  上表格展示异方差White检验和JB检验，分别用于异方差和正态性检验，空间计量模型时对于空间作用的关注力度明显最高，对于异方差和正态性关注度相对较低，从上表格可以看到，并没有异方差差问题，残差也呈现出正态性。如果有异方差问题时，可考虑使用稳健标准误法进行估计即可。

  

  上表格展示信息准则结果表格，包括llf值和另外两个值即AIC值和Schwarz准则值，llf值通常越大越好，但是AIC值和Schwarz准则值均是越小越好，如果希望对比模型优劣，可考虑使用上述三个指标，但需要注意的是，极大似然法估计ML法时才会输出上述指标，如果是比如GMM估计则没有输出上述指标。

  

  上表格展示空间效应分析结果，直接效应ADI反映自变量X对于自身区域Y的平均影响效应情况，间接（溢出）效应AII反应自变量X对其它区域Y的平均影响效应情况，总效应ATI=直接效应ADI+间接（溢出）效应AII。空间杜宾误差模型时，直接效应即为X的回归系数，间接效应为自变量空间滞后变量的回归系数，其计算公式如下：

  

  

  上表格展示模型的简化表格格式，不再重复分析。

• 6、剖析

  • 涉及以下几个关键点，分别如下：

  • 空间杜宾误差模型同时考虑自变量和误差项的空间滞后作用，如果只需要考虑自变量空间滞后作用，可使用自变量空间滞后模型SLX。